Вы точно человек?
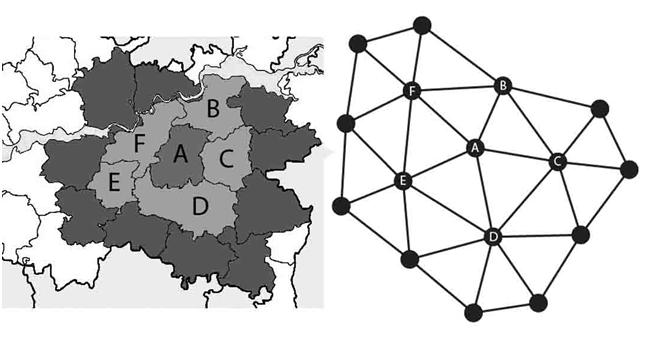
Теорема о четырех цветах — это математический вопрос, который возник еще в 19 веке. Он заключается в том, можно ли раскрасить любую карту, используя только четыре цвета, таким образом, чтобы ни одна из двух соседних областей не имела одинакового цвета. В этом материале мы расскажем, у кого впервые возник этот вопрос, причем тут теория графов, кто и как пытался доказать эту теорему и что из этого вышло. Первоначально вопросом четырех цветов заинтересовался студент Фредерик Гатри, который изучал карту графств Англии. Гатри заметил, что для того, чтобы два соседних графства были разных цветов, необходимо всего четыре цвета. Это наблюдение заставило его задаться вопросом, возможно ли применить этот принцип к любой карте, будь то весь мир, страна или группа островов.






.png)
Категория: Математика. Похожие презентации:. Раскраска графов.
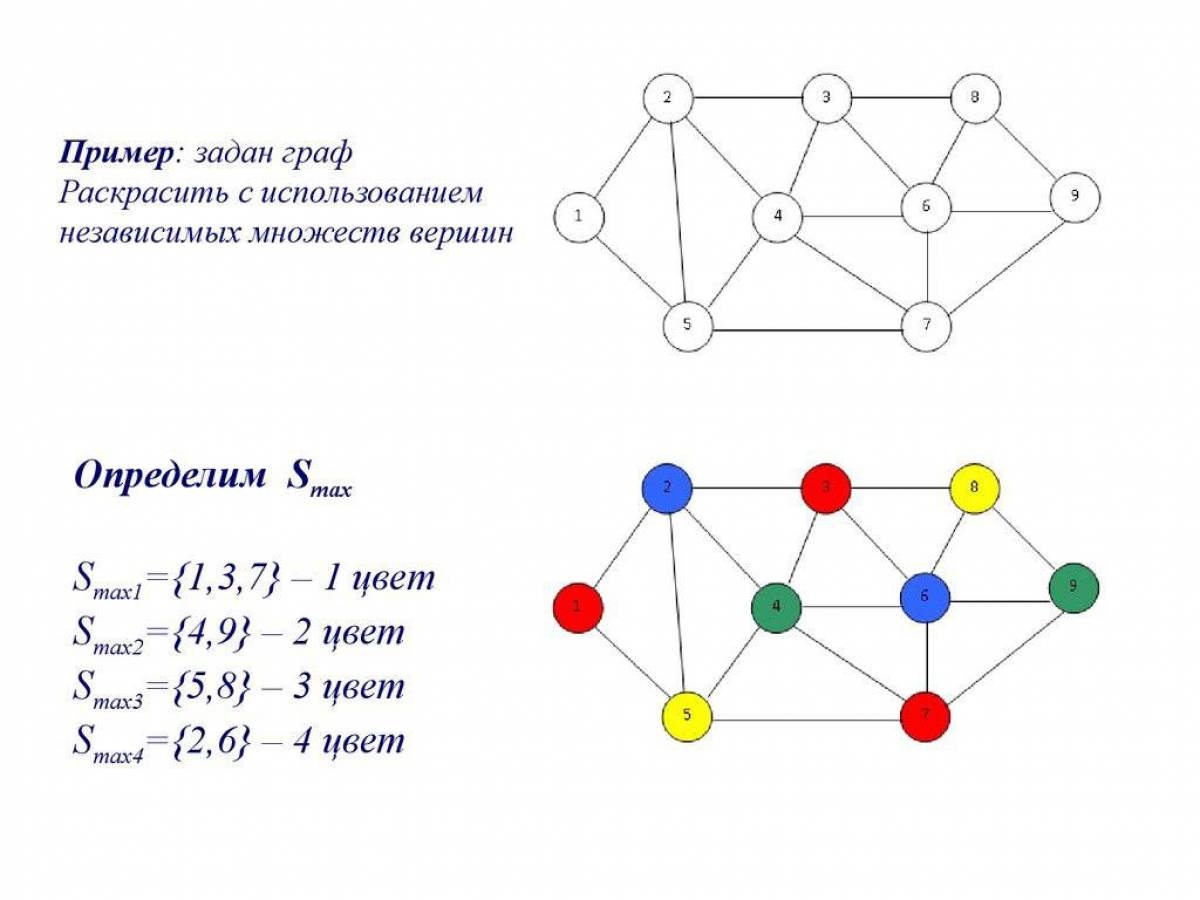






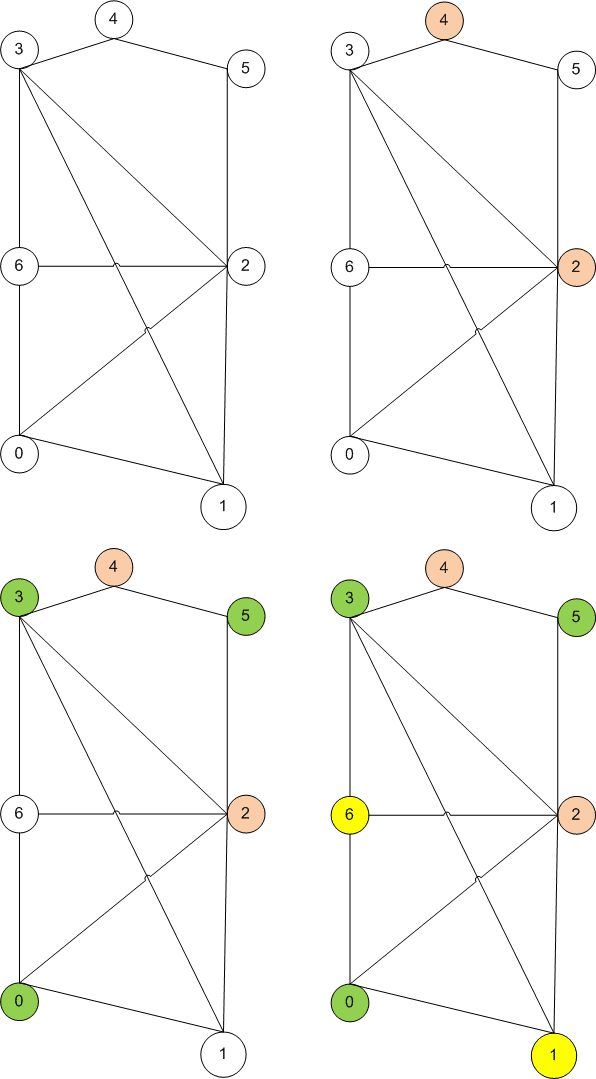

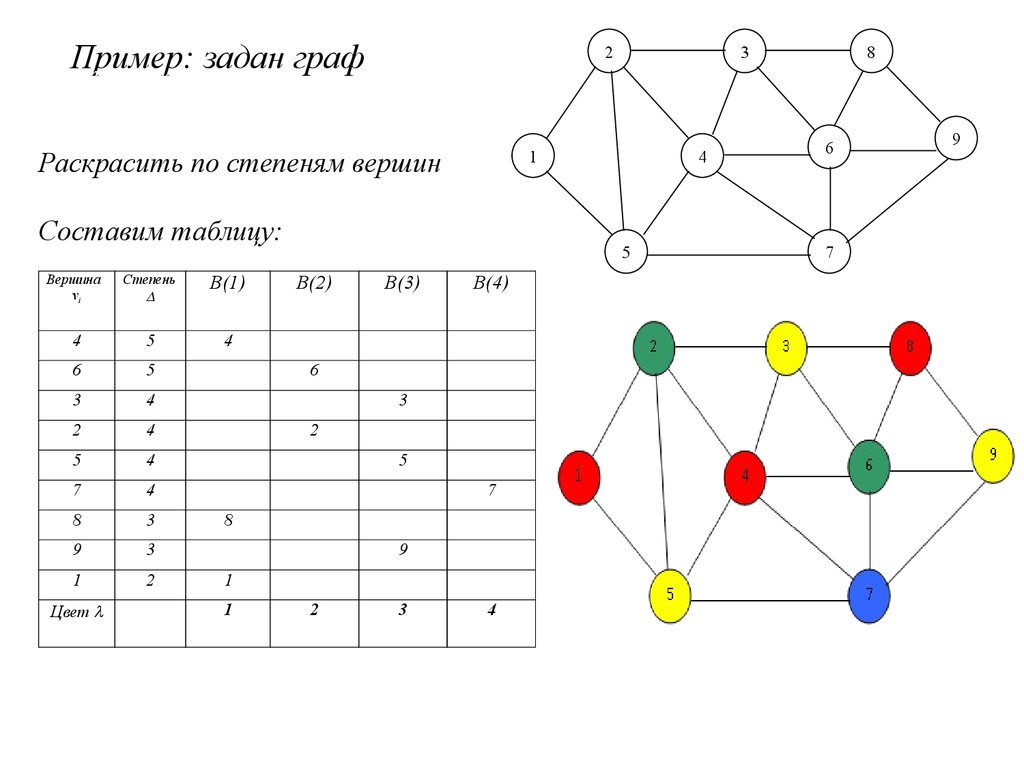
| 426 | Вершины, окрашенные в один цвет, образуют внутреннее устойчивое множество вершин в G. | ||
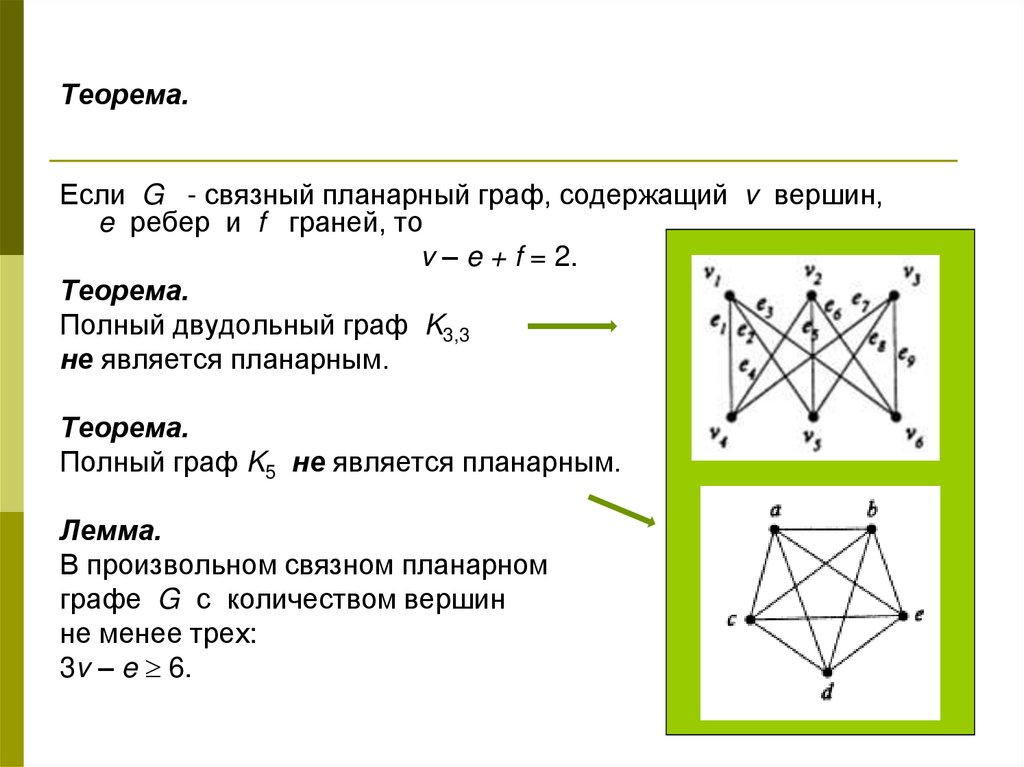
| 85 | Начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. | ||
| 68 | Индукционный переход. Предположим, что правильная 6—раскраска существует для всякого планарного графа порядка N. | ||
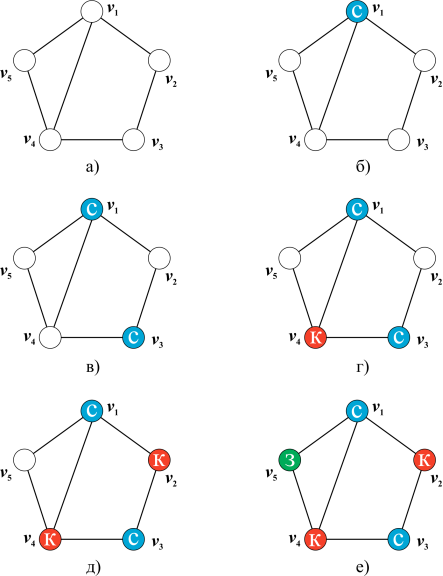
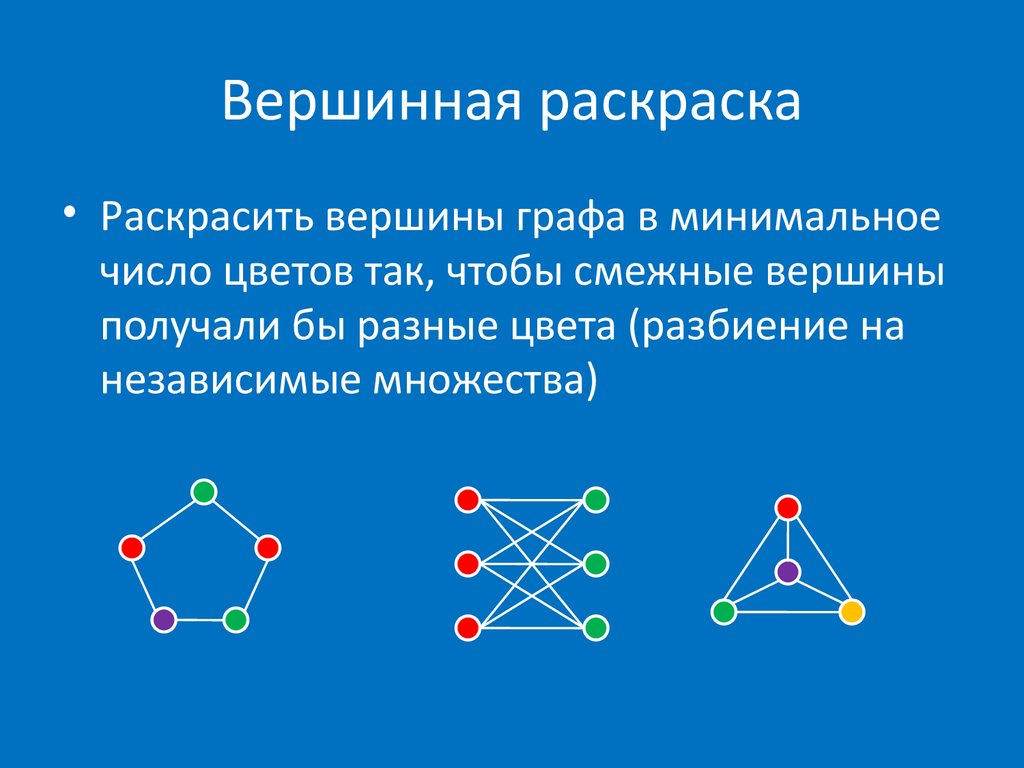
| 149 | На этом шаге мы рассмотрим раскраски графов. Вершинной раскраской далее - просто раскраской графа называется отображение множества вершин графа на конечное множество множество цветов ; n- раскраска графа - раскраска с использованием n цветов. | ||
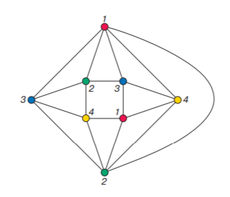
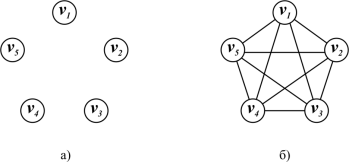
| 298 | При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др. Если между вершинами существует ребро, то соответствующие точки фигуры соединяются отрезком или дугой. |
Для планарного графа можно дать оценку сверху на хроматическое число. Начало доказательства такое же, как в предыдущей теореме, трудность возникает в индукционном переходе. Рассмотрим две необычные ситуации, которые могут наступить во время обхода:. Если этот процесс был успешно завершён, то получили правильную раскраску. Если удастся — раскраска получена. Это была первая крупная математическая теорема, доказанная с помощью компьютера.